Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Sep 13;13(9):e0204056.
doi: 10.1371/journal.pone.0204056. eCollection 2018.

Bias caused by sampling error in meta-analysis with small sample sizes

Lifeng Lin  1
Affiliations

Bias caused by sampling error in meta-analysis with small sample sizes

Lifeng Lin. PLoS One. .

Abstract

Background: Meta-analyses frequently include studies with small sample sizes. Researchers usually fail to account for sampling error in the reported within-study variances; they model the observed study-specific effect sizes with the within-study variances and treat these sample variances as if they were the true variances. However, this sampling error may be influential when sample sizes are small. This article illustrates that the sampling error may lead to substantial bias in meta-analysis results.

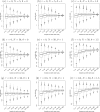
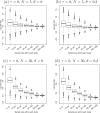
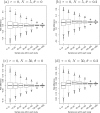
Methods: We conducted extensive simulation studies to assess the bias caused by sampling error. Meta-analyses with continuous and binary outcomes were simulated with various ranges of sample size and extents of heterogeneity. We evaluated the bias and the confidence interval coverage for five commonly-used effect sizes (i.e., the mean difference, standardized mean difference, odds ratio, risk ratio, and risk difference).

Results: Sampling error did not cause noticeable bias when the effect size was the mean difference, but the standardized mean difference, odds ratio, risk ratio, and risk difference suffered from this bias to different extents. The bias in the estimated overall odds ratio and risk ratio was noticeable even when each individual study had more than 50 samples under some settings. Also, Hedges' g, which is a bias-corrected estimate of the standardized mean difference within studies, might lead to larger bias than Cohen's d in meta-analysis results.

Conclusions: Cautions are needed to perform meta-analyses with small sample sizes. The reported within-study variances may not be simply treated as the true variances, and their sampling error should be fully considered in such meta-analyses.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Boxplots of the estimated mean differences in 10,000 simulated meta-analyses.
The true between-study standard deviation τ increased from 0 (panels a and b) to 1 (panel c). The number of studies in each meta-analysis N increased from 5 (panel a) to 50 (panels b and c). The true mean difference Δ (horizontal dotted line) was 0.
Fig 2
Fig 2. Boxplots of the estimated standardized mean differences in 10,000 simulated meta-analyses.
For each sample size range on the horizontal axis, the left gray box was obtained using Cohen’s d, and the right black box was obtained using Hedges’ g. The true between-study standard deviation τ increased from 0 (upper and middle panels) to 0.5 (lower panels). The number of studies in each meta-analysis N increased from 5 (upper panels) to 50 (middle and lower panels). The true standardized mean difference θ (horizontal dotted line) increased from 0 (left panels) to 1 (right panels).
Fig 3
Fig 3. Boxplots of the estimated log odds ratios in 10,000 simulated meta-analyses.
The true between-study standard deviation τ increased from 0 (upper and middle panels) to 0.5 (lower panels). The number of studies in each meta-analysis N increased from 5 (upper panels) to 50 (middle and lower panels). The true log odds ratio θ (horizontal dotted line) increased from 0 (left panels) to 1.5 (right panels).
Fig 4
Fig 4. Boxplots of the estimated log risk ratios in 10,000 simulated meta-analyses.
The true between-study standard deviation τ was 0 (i.e., the simulated studies were homogeneous). The number of studies in each meta-analysis N increased from 5 (upper panels) to 50 (lower panels). The true log risk ratio θ (horizontal dotted line) increased from 0 (left panels) to 0.3 (right panels).
Fig 5
Fig 5. Boxplots of the estimated risk differences in 10,000 simulated meta-analyses.
The true between-study standard deviation τ was 0 (i.e., the simulated studies were homogeneous). The number of studies in each meta-analysis N increased from 5 (upper panels) to 50 (lower panels). The true risk difference θ (horizontal dotted line) increased from 0 (left panels) to 0.2 (right panels).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Sutton AJ, Higgins JPT. Recent developments in meta-analysis. Statistics in Medicine. 2008;27(5):625–50. 10.1002/sim.2934 - DOI - PubMed
    1. Berlin JA, Golub RM. Meta-analysis as evidence: building a better pyramid. JAMA. 2014;312(6):603–6. 10.1001/jama.2014.8167 - DOI - PubMed
    1. Gurevitch J, Koricheva J, Nakagawa S, Stewart G. Meta-analysis and the science of research synthesis. Nature. 2018;555:175–82. 10.1038/nature25753 - DOI - PubMed
    1. Higgins JPT, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557–60. 10.1136/bmj.327.7414.557 - DOI - PMC - PubMed
    1. Higgins JPT, Thompson SG. Quantifying heterogeneity in a meta-analysis. Statistics in Medicine. 2002;21(11):1539–58. 10.1002/sim.1186 - DOI - PubMed

Publication types

LinkOut - more resources