Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Aug 17;13(1):13361.
doi: 10.1038/s41598-023-40466-1.

Structure-based modeling of critical micelle concentration (CMC) of anionic surfactants in brine using intelligent methods

Danial Abooali  1 , Reza Soleimani  2
Affiliations

Structure-based modeling of critical micelle concentration (CMC) of anionic surfactants in brine using intelligent methods

Danial Abooali et al. Sci Rep. .

Abstract

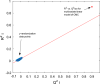
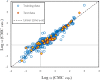
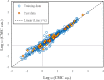
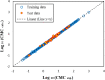
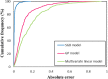
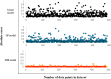
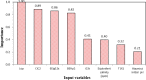
Critical micelle concentration (CMC) is one of the main physico-chemical properties of surface-active agents, also known as surfactants, with diverse theoretical and industrial applications. It is influenced by basic parameters such as temperature, pH, salinity, and the chemical structure of surfactants. Most studies have only estimated CMC at fixed conditions based on the surfactant's chemical parameters. In the present study, we aimed to develop a set of novel and applicable models for estimating CMC of well-known anionic surfactants by considering both the molecular properties of surfactants and basic affecting factors such as salinity, pH, and temperature as modeling parameters. We employed the quantitative-structural property relationship technique to employ the molecular parameters of surfactant ions. We collected 488 CMC values from literature for 111 sodium-based anionic surfactants, including sulfate types, sulfonate, benzene sulfonate, sulfosuccinate, and polyoxyethylene sulfate. We computed 1410 optimized molecular descriptors for each surfactant using Dragon software to be utilized in the modelling processes. The enhanced replacement method was used for selecting the most effective descriptors for the CMC. A multivariate linear model and two non-linear models are the outputs of the present study. The non-linear models were produced using two robust machine learning approaches, stochastic gradient boosting (SGB) trees and genetic programming (GP). Statistical assessment showed highly applicable and acceptable accuracy of the newly developed models (RSGB2 = 0.999395 and RGP2 = 0.954946). The ultimate results showed the superiority and greater ability of the SGB method for making confident predictions.

PubMed Disclaimer

Conflict of interest statement

The authors certify that they have NO conflict over any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Figures

Figure 1
Figure 1
The effect of number of molecular descriptors on the prediction capability in descriptors selection step.
Figure 2
Figure 2
The graph of RMSD over the successive boosting steps for the training and test samples using SGB method.
Figure 3
Figure 3
The effects of learning rate on the performance of the SGB model for predicting CMC.
Figure 4
Figure 4
Schematic of a simple GP gene including the operators: + , ^, × , tanh.
Figure 5
Figure 5
The result of y-randomization test for multi-variable linear model of CMC.
Figure 6
Figure 6
The estimated CMC versus experimental data for multivariate linear model over training and test datasets.
Figure 7
Figure 7
The estimated CMC versus experimental values for GP model over training and test datasets.
Figure 8
Figure 8
The estimated CMC versus experimental values for SGB model over training and test datasets.
Figure 9
Figure 9
Cumulative frequency of the new developed models.
Figure 10
Figure 10
Absolute errors of data points over all dataset for linear model (top), GP model (middle) and SGB model (down). It is observed that the estimation accuracy has been increased from top to down.
Figure 11
Figure 11
Relative importance of independent variables on the CMC based on the SGB algorithm.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Schramm LL, Stasiuk EN, Marangoni DG. 2 Surfactants and their applications. Ann. Rep. Sect. C (Phys. Chem.) 2003;99:3–48. doi: 10.1039/B208499F. - DOI
    1. Massarweh O, Abushaikha AS. The use of surfactants in enhanced oil recovery: A review of recent advances. Energy Rep. 2020;6:3150–3178. doi: 10.1016/j.egyr.2020.11.009. - DOI
    1. Suárez L, Díez MA, García R, Riera FA. Membrane technology for the recovery of detergent compounds: A review. J. Ind. Eng. Chem. 2012;18:1859–1873. doi: 10.1016/j.jiec.2012.05.015. - DOI
    1. Falbe, J. Surfactants in Consumer Products: Theory, Technology and Application. (Springer Science & Business Media, 2012).
    1. Hellgren A-C, Weissenborn P, Holmberg K. Surfactants in water-borne paints. Prog. Org. Coat. 1999;35:79–87. doi: 10.1016/S0300-9440(99)00013-2. - DOI