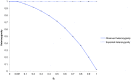
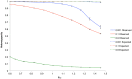
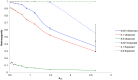
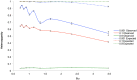
Computational models of evolutionary processes are increasingly required to incorporate multiple and diverse sources of data. A popular feature to include in population genetics models is spatial extension, which reflects more accurately natural populations than does a mean field approach. However, such models necessarily violate the mean field assumptions of classical population genetics, as do natural populations in the real world. Recently, it has been questioned whether classical approaches are truly applicable to the real world. Individual based models (IBM) are a powerful and versatile approach to achieve integration in models. In this study an IBM was used to examine how populations of plants deviate from classical expectations under spatial extension. Populations of plants that used three different mating strategies were placed in a range of arena sizes giving crowded to sparse occupation densities. Using a measure of population density, the pollen communication distance (P(cd)), the deviation exhibited by outbreeding populations differed from classical mean field expectations by less than 5% when P(cd) was less than 1, and over this threshold value the deviation significantly increased. Populations with an intermediate mating strategy did not have such a threshold and deviated directly with increasing isolation between individuals. Populations with a selfing strategy were influenced more by the mating strategy than by increased isolation. In all cases pollen dispersal was more influential than seed dispersal. The IBM model showed that mean field calculations can be reasonably applied to natural outbreeding plant populations that occur at a density in which individuals are less than the average pollen dispersal distance from their neighbors.